[조길영 교수 연구실] Many-Body Invariants for Chern and Chiral Hinge Insulators
- 첨부된 파일이 없습니다.
관련링크
본문
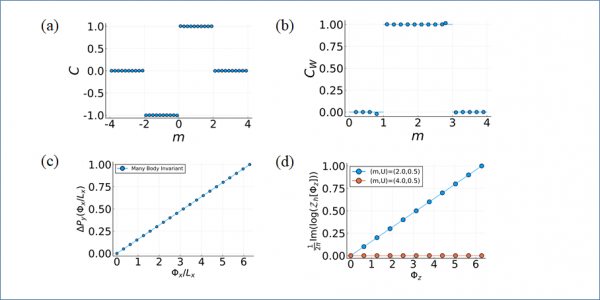
Caption: (a) 다체불변량(Many-body invariant)를 사용한 천 부도체(Chern insulator) 및 (b) 모서리 부도체 (Hinge insulator)의 상 분류. (c) 천 부도체와 (d) 모서리 부도체의 다체불변량을 그래프 위의 두 점이 주는 기울기로 부터 알 수 있다.
포스텍(포항공대) 조길영 교수 연구팀이 강상 위상 상태를 분류하는 효과적인 방법을 발견했다.
물리학과 조길영 교수 연구팀은 고차위상상태를 다체불변량(Many-body invariants)를 통해 분류할 수 있으며 다체불변량을 기존의 방식보다 적은 정보를 사용해 계산해낼 수 있음을 보였다. 이 연구는 미국 물리학회의 저명 학술지인 Physical Review Letters 최신호에 게재됐다. 이번 연구는 고차위상상태에 대한 통합된 시각을 제공했을 뿐만이 아니라 고차위상상태를 보다 효과적인 방식으로 연구할 수 있는 아이디어를 제시한 연구로 평가된다.
위상 부도체는 양자화된 비대칭 전하 운반(quantized chiral charge pumping)에 의해서 분류된다. 위상 부도체중 하나인 천 부도체(Chern insulator)는 운반되는 전하의 양이 천 수(Chern number)로 정해진다는 사실이 알려져 있다. 본 연구에서는 이것을 확장하여 고차위상부도체에 대한 천 숫자로써 다체불변량(Many-body invariants)을 제안했고, 예시로 고차위상부도체 중 하나인 “모서리 부도체(Hinge insulator)”에 대해서 다체불변량을 계산하였다. 또한 다체불변량이 양자화된 다중극자의 운반에 해당함을 확인하였다. 한편, 천 숫자를 포함해 다체불변량을 계산하기 위해서는 일반적으로 많은 수의 기저상태 계산을 필요하다. 하지만 본 연구에서는 단 두 개의 기저상태만을 사용하여서 다체불변량을 계산하는 방법을 제안하고 있으며, 연구를 주도한 조길영 교수는 “현재 연구를 통해 강상 위상 물질의 효율적 탐색이 가능해질 것”이라고 밝혔다.


-2.gif)








 Login
Login


